DP Finite Automata with Compression: Artillery Position
The generals plan to deploy their artillery troops on a grid map of N × M.
Each cell may be a map of the mountain (with H representation), it may be plain (with P representation), as shown below.
At most one artillery unit can be deployed on each grid of plain terrain (P) and artillery units cannot be deployed on mountainous terrain (H); the attack range of an artillery unit on the map is shown in the black area in the figure:
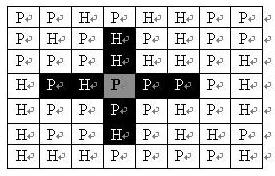
If an artillery unit is deployed on the plain marked by gray in the map, the black grid in the figure indicates the area it can attack: two squares in the horizontal direction and two squares in the vertical direction.
None of the other white grids on the map can be attacked.
It can be seen from the picture that the attack range of the artillery is not affected by the terrain.
Now, the generals plan how to deploy artillery units, under the premise of preventing accidental injury (ensure that no two artillery units can attack each other, that is, any artillery unit is not within the attack range of other artillery units) in the entire map. Find the maximum number of artillery units that can be placed in the area.
Input format
The first line contains two positive integers separated by spaces, which represent N with M;
Next N Rows, each row contains consecutive M characters ( P or H) without spaces. Represents the data of each row in the map in order.
Output format
Only one line, contains an integer K, Which indicates the maximum number of artillery units that can be placed.
data range N≤ 100 , M≤ 10
Input sample:
Sample Input:
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
Sample Output:
6
Solution
dp[i][j][k]: the maximum number of artilleries placed
- i: current row,
- j: the placement of artilleries in row i
- k: the placement of artilleries in row i - 1
dp[i][j][k] = max(dp[i][j][k], dp[i-1][k][u] + cnt[j])
Optimization:
- We use a rolling array to compress the first dimension to 2 since only i-1 values are needed.
- We add valid j to a list state[] and enumerate that list for all possible i, i-1, i-2 rows
dp[i%2][state[j]][state[k]] = max(dp[i%2][state[j]][state[k]], dp[(i-1)%2][state[k]][state[u]] + cnt[state[j]])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int N=110,M=10,S=1<<M;
int n,m;
int g[N];
//dp[2] is needed since only i and i-1 are needed
int dp[2][S][S];
vector<int>state;
int cnt[S];
// check if placement of artilleries in this row is valid
bool check(int s){
for(int i=0;i<m;i++)
//for each i column, check left 2 positions
if((s>>i&1)&&((s>>i+1&1)||(s>>i+2&1)))
return false;
return true;
}
// count number of artilleries in this row
int count(int s){
int res=0;
while(s){
res+=s&1;
s>>=1;
}
return res;
}
int main(){
cin>>n>>m;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++){
char c;
cin>>c;
if(c=='H')g[i]+=1<<j;
}
}
//add all valid row artilleries placement into a list
for(int i=0;i<1<<m;i++)
if(check(i)){
state.push_back(i);
cnt[i] = count(i);
}
for(int i=0;i<n+2;i++)
//enumerate all possible i-th row placement
for(int j=0;j<state.size();j++)
//enumerate all possible valid i - 1 and i - 2 row placement
for(int k=0;k<state.size();k++)
for(int u=0;u<state.size();u++){
int a=state[j],b=state[k],c=state[u];
//check there are two artilleries placed in the same column
//thus resulting an invalid placement, in any of these two rows
if((a&b)||(a&c)||(b&c))
continue;
//for i-th row value state[i] and i -1 row state[k], make sure all artilleries placed on P (plain)
if((g[i] & a) != 0 || (g[i-1] & b) != 0) continue;
continue;
dp[i%2][j][k] = max(dp[i%2][j][k], dp[(i-1)%2][k][u] + cnt[a]);
}
cout<<f[n+1%2][0][0];
return 0;
}