Dynamic Programming: Knapsack with Multiple Contstraits
Have N Kinds of items and a capacity are V Backpack.
First i There are at most si Pieces, the volume of each piece is vi, The value is wi.
Solve which items are loaded into the backpack, so that the total volume of the items does not exceed the capacity of the backpack, and the total value is the largest.
Output the maximum value.
Input format Two integers in the first line,N, V ( 0 < N≤ 1000, 0 < V≤ 20000 ), Separated by spaces, respectively indicate the number of objects and the volume of the backpack.
Next there is N Lines, three integers per line vi,wi,si, Separated by spaces, indicating the first i The volume, value, and quantity of various items.
Output format Output an integer that represents the maximum value.
data range 0 < N≤ 1000 0 < V≤ 20000 0 <vi,wi,si≤ 20000
Sample Input:
4 5
1 2 3
2 4 1
3 4 3
4 5 2
Sample Output:
10
Solution 1
Monotonous queue of multiple backpacks
dp[i][j] represents the maximum value that can be obtained when only the first i items are considered and the backpack capacity is j
Transfer formula: dp[i][j] = max(dp[i-1][j], dp[i-1][j-kc] + kw), 1≤k≤s = max(dp[i- 1][j-kc] +kw), 0≤k≤s
The transfer table is as follows:
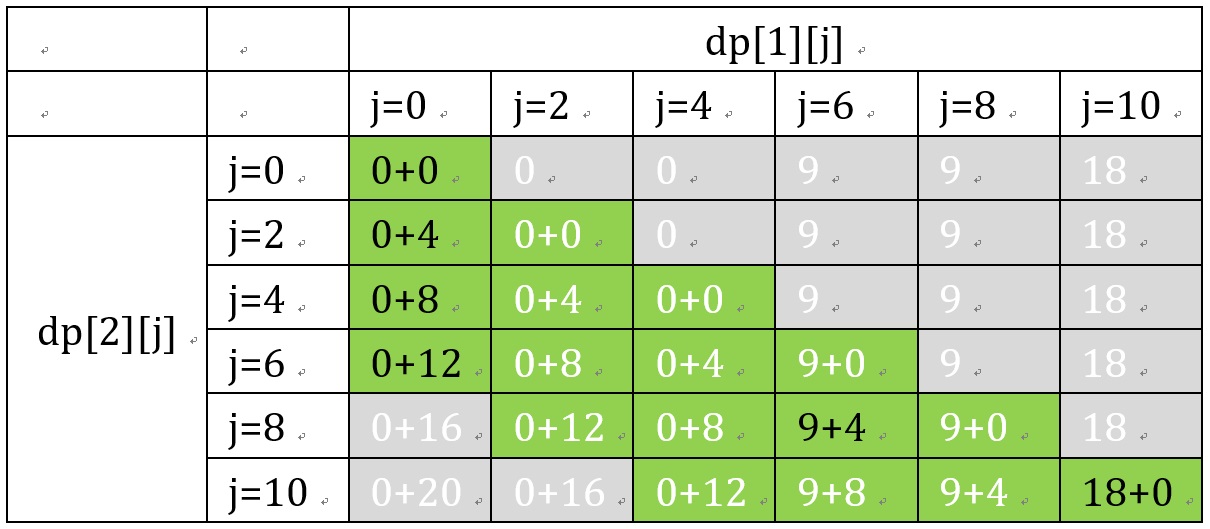
When only considering dp[2][1]
Green means: backpack capacity v% item space c = 0
Orange means: backpack capacity v% item space c = 1
Green is only updated from the upper layer of green, and orange is only updated from the upper layer of orange
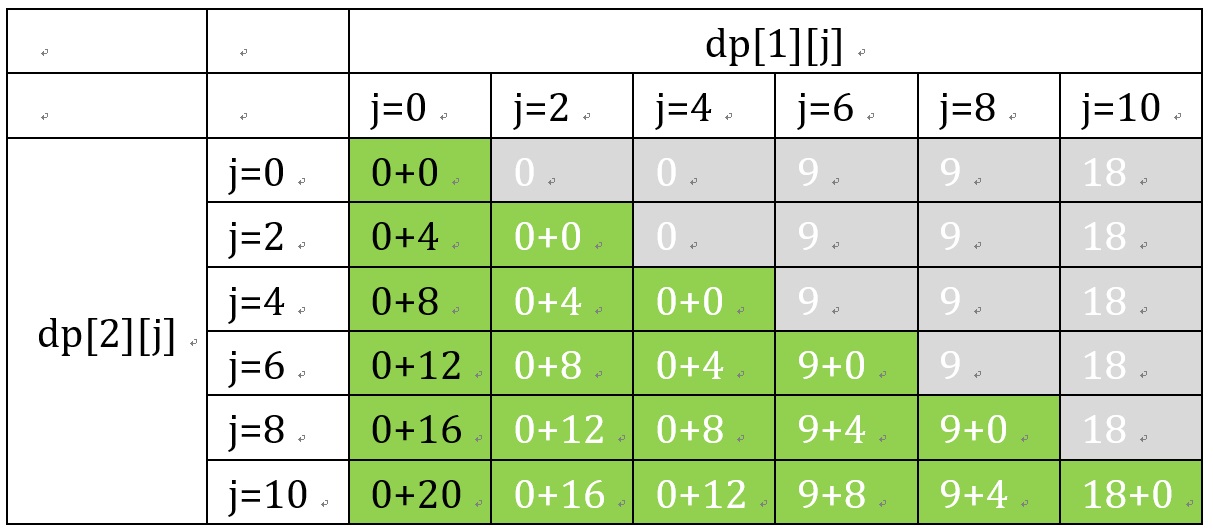
Only consider the transfer process of green blocks
Green represents the effective area, and gray represents the ineffective area (because it can only be moved backwards, or the number of items is limited). The limit on the number of items can also be understood as having at most s+1 elements in each row.
The black font represents the maximum value of the line
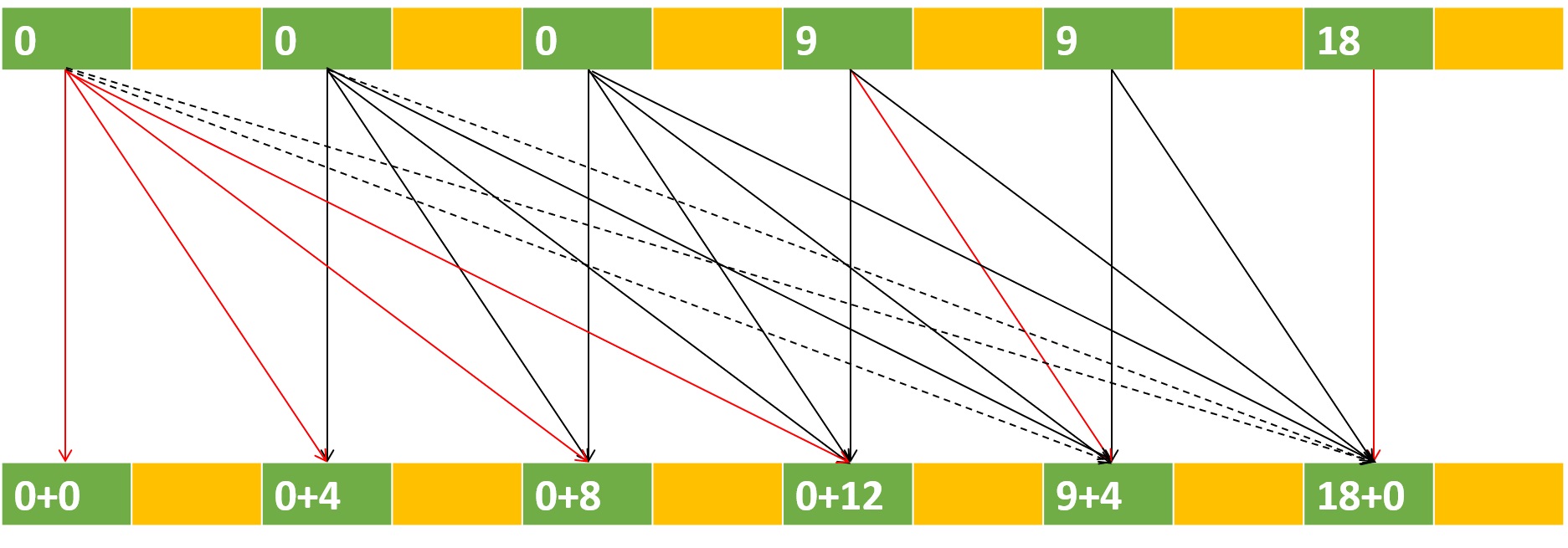
The process in the above figure can be achieved through a monotonic queue
Look at the transfer process from another perspective The dotted line represents the invalid transfer caused by the limit on the number of items
The solid line represents effective transfer
Red represents the maximum transfer

got the answer
Another angle of the complete knapsack problem The transition diagram of the complete knapsack problem is the same as that of the multiple knapsacks. However, there is no limit on the number of items, so it is not a sliding window situation, and there is no need for a monotonous queue. Only save a maximum value.
It is not necessarily all transferred by dp[1][0], but the example happens to be so
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
#include <cstring>
using namespace std;
const int N = 20010;
int dp[N], pre[N], q[N];
int n, m;
int main() {
cin >> n >> m;
for (int i = 0; i < n; ++i) {
memcpy(pre, dp, sizeof(dp));
int v, w, s;
cin >> v >> w >> s;
for (int j = 0; j < v; ++j) {
int head = 0, tail = -1;
for (int k = j; k <= m; k += v) {
if (head <= tail && k - s*v > q[head])
++head;
while (head <= tail && pre[q[tail]] - (q[tail] - j)/v * w <= pre[k] - (k - j)/v * w)
--tail;
if (head <= tail)
dp[k] = max(dp[k], pre[q[head]] + (k - q[head])/v * w);
q[++tail] = k;
}
}
}
cout << dp[m] << endl;
return 0;
}
Solution 2: Recursive DP
Imagine that we had a magical function knapsack(item,weight,volume) that could return the largest valid value of items that could be taken given the item number, weight and volume.
The solution would then iterate though every item after it and see what the answer would be and take the largest one. Similar to the 1/0 DP that you do.
However, you realize that you don’t need to keep track of the volume in the dp array hence it being only 2D.
You only need to keep track of the volume at the end when you see that there are no more items that can be taken.
A pretty standard solution for 1/0 Knapsack with a slight modification using recursive DP.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
int knapsack(int item, int weight, int volume) {
// See if we have calculated this item before
if (dp[item][weight] == -1) {
// Set initial value to -2 (invalid result)
int max = -2;
// Iterate though all items past current item
for (int i = item; i < n; i++) {
// Make sure we don't go over max weight
if (weight + w[i] <= W_max) {
// Get the result of taking ith item
int res = knapsack(i + 1, weight + w[i], volume + vol[i]);
// Make sure result is valid (Total volume is greater than Vol_min)
if (res != -2) {
// If the result is valid take the max
max = Math.max(res + val[i], max);
}
}
}
// No other items taken and over Vol_min
if (max == -2 && volume >= Vol_min)
dp[item][weight] = 0;
else // Eveything else
dp[item][weight] = max;
}
// Return the value
return dp[item][weight];
}